Introduction to Music and Music Theory.
A World of Sound.
A world of Sound! Isn't that fantastic to imagine that a vibrating object such as a crystal glass, a string, or a piece of resonance wood, can produce a series of waves and thus sound, called Harmonic. For instance, a string, from its fundamental "Tonic" has about 15-16 more harmonics decreasing in intensity and in sections as well. If these smaller lengths are integer fractions (1/2, 1/3,1/4, ...) of the total length of the string, their frequencies of oscillation are called harmonics and are integer multiples of the fundamental.
Why am I talking of theses Harmonic series? When examining in detail the graph above, you'll see that our vibrating string, gives all the notes involved in a chord. Effectively, one has some Tonics C, some Dominants G, then Thirds, and so on. Even a seventh harmonic B flat. However, this B flat is here a little bit too flat. We know now, that the total sound of a string is the sum of all the harmonics present. If the 7th overtone is present, and it’s played with other notes from the scale (especially the min7th) it’ll sound really dissonant and out-of-tune. That’s why the hammers in a piano are generally located near a node of the 7th overtone.
Image of a reasoning crystal tube form, giving harmonic sounds. Picture taken in the Vienna Music Museum.
Ancient Greek music theory.
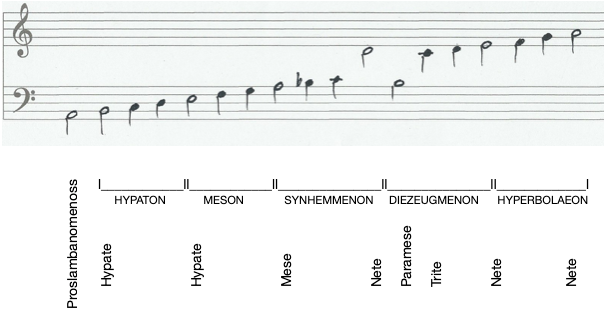
According to Pythagoras (570 – 495 BC) doctrine, the world must be harmoniously ordained, the celestial bodies which are distant from one another according to the proportions of consonant sound, create, by the movement and speed of their revolutions, the corresponding harmonic sounds. The Greek scale on a linear Zodiac.
On the other hand, one could begin with the meanings of the single tones and bend the double-octave into a circle, joining nete hyperbolaion (Media, A,E,D note) and proslambanomenos, (Aquisitus, D note) and uniting the two tones. This juncture will then lie diametrically opposite the mese and be in octave relationship to it.
Pythagoras is generally credited with having discovered that musical intervals which are recognized as concordant are related by small integer ratios, an idea he may have acquired from Babylon. It is likely that he determined this result using a monochord, a single-stringed instrument having a moveable bridge by means of which the string can be divided into two parts of variable proportion. Strings with lengths in the ratio 2 : 1 produced the interval of an octave known to the ancient Greeks as diapason, Those in the proportion 3 : 2 produced the interval of the fifth, known to the Greeks as diapente. Strings of equal tension with length in the proportion 4 : 3 produced the interval of a fourth known to the Greeks as diatessaron. The Greek word dia meant between, through or across. All of these intervals are present between strings with relative lengths 2, 3 and 4. Thus the most harmonious of intervals are contained in the number progression 1 : 2 : 3 : 4. This reinforced the concept of spacial and musical harmony being related and the belief that the harmony of the entire universe was inherent in the mystical power of numbers. Pythagoras himself left no written record of his work so it was via his pupil Philolaus that these observations have been passed on. The first record of the use of a monochord to demonstrate this phenomena was by Euclid (c. 300 B.C.).
Gradus ad Parnassum
In Greek mythology, one of the peaks was sacred to Apollo and the nine Muses (Music) the inspiring deities (religious iconography) of the arts, and the other to Dionysus.
Alexander the great verses.
The Earth at the center gives the low sound of the hypate; the starry sphere gives the conjunct nete: the Sun placed in the middle of the errant stars gives the mese; the crystal sphere gives the fourth in relation to it; Saturn is lowest by a half-tone; Jupiter diverges as much from Saturn as from the terrible Mars; the Sun, joy of mortals, is one tone below; Venus differs from the dazzling sun by a trihemitone; Hermes continues with a half-tone lower than Venus; then comes the Moon which gives to nature such varying hue; and finally, the Earth at the center gives the fifth with respect to the Sun; and this position has five regions, from wintry to torrid, accommodating itself to the most intense heat, as to the most glacial cold. The Heavens, which contain six tones, complete the octave. The son of Jupiter, Hermes, represents a Siren to us, having a seven stringed lyre, the image of this divine world.