Note Intervals
What are note intervals in music
- The difference between two sounds/pitches is called, harmonic interval.
- Intervals are named by size and quality.
- Interval qualities are major (M), minor (m), perfect (P), diminished (º) and augmented (+).
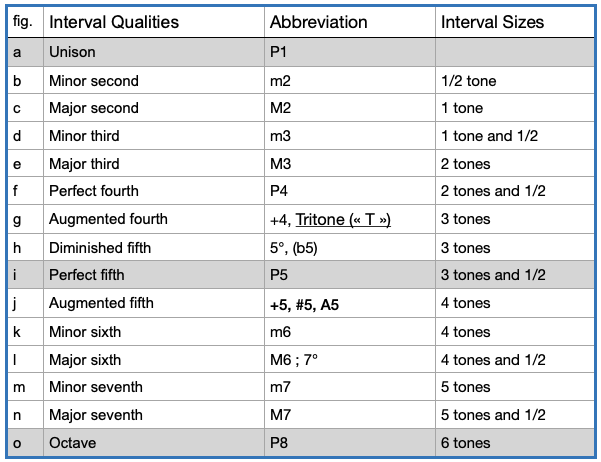
- Interval Size: distance between two given notes. (see table below)
- Intervals that are 2, 3, 6, or 7 in size can be major, minor, diminished or augmented. These intervals can never be perfect.
- Intervals that are 1, 4, 5, or 8 in size can be perfect, diminished or augmented. These intervals can never be major or minor.
- The picture below shows the simple intervals from C to any notes above.
Simple Intervals.
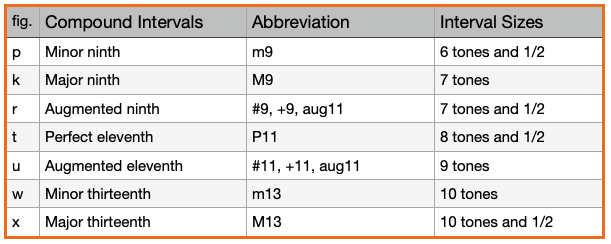
Compound Intervals
Compound intervals are intervals larger than an octave. (Above 6 tones). The first ligne below shows the number of semitones. From a to x are the figure references shown in the tables below. Compound intervals are functionally the same as the corresponding simple intervals (those an octave or less in size). Thus, a 9th is a compound 2nd (M9), an 11th is a compound 4th (P11) and a 13th is compound 6th (M13).
Consonance and Dissonance Intervals
- Consonant intervals are those intervals that sound stable and usually pleasant to the ear. (m3, M3, P4, P5, m6, M6, P8 (octave))
- Dissonant intervals are those that sound harsh and unstable, they feel as if they want to resolve: (m2, M2, m7, M7, Tritone (augmented fourth)
- The P1, P8, and P5 are known as perfect consonances.
- The m3, m6, m7, M2, M3, M6 are known as imperfect consonances.
Some thoughts about music note intervals.
According to Hindemith and generally speaking, the consonant intervals excel in harmonic power, the dissonant intervals in melodic power, whereas the tritone is considered apart, as possessing specifically, neither harmonic nor melodic significance. The term root is applied not only to chords but also to intervals. In the perfect fifth, major and minor thirds, and major and minor seventh, the root tone of the interval is the lower tone; in the perfect fourth, major and minor sixths, and major and minor seconds, the root tone is the upper tone of the interval. The fundamental of a chord is found by first selecting the "best" interval between any two tones of the chord, the intervals being arranged in a series to decreasing value from the perfect fifth to the major seventh.